Understand the mathematics behind noise suppression
In this section, you will learn about the mathematics that serves as a basis for the use case. Then, you will use those principles to create a reference implementation using NumPy.
Overlapping windows
The blocks of audio samples you created in the previous steps will be multiplied by a Hanning window function, which you will achieve by running the following in the Jupyter notebook:
window=dsp.arm_hanning_f32(winLength)
plt.plot(window)
plt.show()
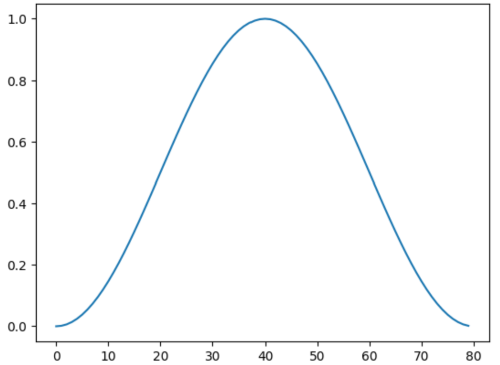Hanning Window
The slices you created are overlapping. By applying a Hanning window function and summing the slices, you can reconstruct the original signal.
Indeed, summing two Hanning windows shifted by half the width of the sample block gives:
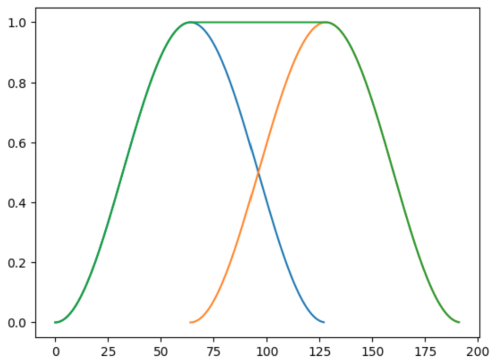Summed Hanning Window
As a result, if you multiply the overlapping blocks of samples by Hanning windows and sum the result, you can reconstruct the original signal:
offsets = range(0, len(data),winOverlap)
offsets=offsets[0:len(slices)]
res=np.zeros(len(data))
i=0
for n in offsets:
res[n:n+winLength] += slices[i]*window
i=i+1
plt.plot(res)
plt.show()
You can now listen to the recombined signal:
audio2=Audio(data=res,rate=samplerate,autoplay=False)
audio2
This means you can process each slice independently and then recombine them at the end to produce the output signal.
How the noise reduction works
The algorithm operates in the spectral domain, using a Fast Fourier Transform (FFT) to analyze the signal. When no speech is detected (based on the VAD), the algorithm estimates the noise level in each frequency band. When speech is present, that noise estimate is used to filter the signal.
Each band is filtered using a simplified Wiener filter, which applies a gain to the signal defined as:
$$H(f) = \frac{S(f)}{S(f) + N(f)}$$- \(S(f)\) is the speech spectrum.
- \(N(f)\) is the noise spectrum.
For this tutorial, you can assume a high Signal-to-Noise Ratio (SNR). The VAD relies on this assumption: the signal energy is sufficient to detect speech. With a high SNR, the transfer function can be approximated as:
$$H(f) \approx 1 - \frac{N(f)}{S(f)}$$You don’t have access to \(S(f)\), only to the measured \(S(f) + N(f)\) which will be used under the assumption that the noise is small, making the approximation acceptable:
$$H(f) \approx 1 - \frac{N(f)}{S(f) + N(f)}$$with \(S(f) + N(f) = E(f)\)
- \(E(f)\) is the observed energy in a frequency band.
It can be rewritten as:
$$H(f) \approx \frac{E(f) - N(f)}{E(f)}$$- \(N(f)\) is estimated when there is no speech.
In the Python code below, you’ll see this formula implemented. Don’t run this snippet in your Jupyter notebook — it will be run later as part of the full implementation.
scaling = (energy - self._noise)/energy
NoiseSuppression and NoiseSuppressionReference classes
The entire algorithm will be packaged as a Python class.
The class functions are explained below using Python code that should not be evaluated in the Jupyter notebook. You should only evaluate the full class definition in the Jupyter notebook—not the code snippets used for explanation.
NoiseSuppression constructor
NoiseSuppression is a shared class used by both the float reference implementation and the Q15 version.
class NoiseSuppression():
def __init__(self,slices):
self._windowLength=len(slices[0])
self._fftLen,self._fftShift=fft_length(self._windowLength)
self._padding_left=(self._fftLen - self._windowLength)//2
self._padding_right=self._fftLen- self._windowLength-self._padding_left
self._signal=[]
self._slices=slices
self._window=None
The constructor for NoiseSuppression:
- Uses the audio slices as input.
- Computes the FFT length that can be used for each slice.
- Computes the padding needed for the FFT.
Because FFTs require a power-of-two length, the constructor computes the smallest power of two greater than the window size and pads the signal accordingly.
NoiseSuppressionReference constructor
class NoiseSuppressionReference(NoiseSuppression):
def __init__(self,slices):
NoiseSuppression.__init__(self,slices)
# Compute the VAD signal
self._vad=clean_vad([signal_vad(w) for w in slices])
self._noise=np.zeros(self._fftLen)
# The Hann window
self._window=dsp.arm_hanning_f32(self._windowLength)
The constructor for NoiseSuppressionReference:
- Uses the audio slices as input.
- Calls the constructor for
NoiseSuppression. - Computes the VAD signal for the full audio signal.
- Compute the Hanning window.
Subnoise
Calculates the approximate Wiener gain and it is applied to all frequency bands of the FFT. The v argument is a vector. If the gain is negative, it is set to 0. A small value is added to the energy to avoid division by zero.
def subnoise(self,v):
# Wiener estimate
energy = v * np.conj(v) + 1e-6
scaling = (energy - self._noise)/energy
scaling[scaling<0] = 0
return(v * scaling)
Remove_noise
Computes the FFT (with padding) and reduces noise in the frequency bands using the approximate Wiener gain.
The function also uses window_and_pad, which is implemented in the final code-block later.
At a glance, this helper method takes care of padding the signal for a basic even-length window, ensuring it runs smoothly with the FFT.
def remove_noise(self,w):
sig=self.window_and_pad(w)
# FFT
fft=np.fft.fft(sig)
# Noise suppression
fft = self.subnoise(fft)
# IFFT
res=np.fft.ifft(fft)
# Assume the result is real - ignore the imaginary part
res=np.real(res)
# Remove the padding
res=self.remove_padding(res)
return(res)
Estimate_noise
If no speech detected, this function is called to estimate the noise energy.
def estimate_noise(self,w):
# Compute the padded signal
sig=self.window_and_pad(w)
fft=np.fft.fft(sig)
# Estimate the noise energy
self._noise = np.abs(fft)*np.abs(fft)
# Remove the noise
fft = self.subnoise(fft)
# IFFT and assume the result is real - ignore imaginary part
res=np.fft.ifft(fft)
res=np.real(res)
res=self.remove_padding(res)
return(res)
Remove_noise_from_slices
This is the main function that removes noise from each slice. If a slice doesn’t contain speech, the noise estimate is updated before applying noise reduction.
def remove_noise_from_slices(self):
for (w,v) in zip(self._slices,self._vad):
result=None
if v==1:
# If voice is detected, only remove the noise
result=self.remove_noise(w)
else:
# If no voice is detected, update the noise estimate
result=self.estimate_noise(w)
self._signal.append(result)
Overlap_and_add
The filtered slices are recombined using the pre-defined window lengths from before:
def overlap_and_add(self):
offsets = range(0, len(self._signal)*winOverlap,winOverlap)
offsets=offsets[0:len(self._signal)]
res=np.zeros(len(data))
i=0
for n in offsets:
res[n:n+winLength]+=self._signal[i]
i=i+1
return(res)
Run the Python class
It’s time to put together the reference version of the noise suppression algorithm. Copy and evaluate this code in your Jupyter notebook.
def fft_length(length):
result=2
fft_shift=1
while result < length:
result = 2*result
fft_shift = fft_shift + 1
return(result,fft_shift)
class NoiseSuppression():
def __init__(self,slices):
self._windowLength=len(slices[0])
self._fftLen,self._fftShift=fft_length(self._windowLength)
self._padding_left=(self._fftLen - self._windowLength)//2
self._padding_right=self._fftLen- self._windowLength-self._padding_left
self._signal=[]
self._slices=slices
self._window=None
# Pad the signal with zeros. The FFT length is greater than the window length and must be a power of 2
def window_and_pad(self,w):
if w.dtype==np.int32:
w=dsp.arm_mult_q31(w,self._window)
elif w.dtype==np.int16:
w=dsp.arm_mult_q15(w,self._window)
else:
w = w*self._window
sig=np.hstack([np.zeros(self._padding_left,dtype=w.dtype),w,np.zeros(self._padding_right,dtype=w.dtype)])
return(sig)
def remove_padding(self,w):
return(w[self._padding_left:self._padding_left+self._windowLength])
class NoiseSuppressionReference(NoiseSuppression):
def __init__(self,slices):
NoiseSuppression.__init__(self,slices)
# Compute the VAD signal
self._vad=clean_vad([signal_vad(w) for w in slices])
self._noise=np.zeros(self._fftLen)
# The Hann window
self._window=dsp.arm_hanning_f32(self._windowLength)
# Subtract the noise
def subnoise(self,v):
# Wiener estimate
energy = v * np.conj(v) + 1e-6
scaling = (energy - self._noise)/energy
scaling[scaling<0] = 0
return(v * scaling)
def remove_noise(self,w):
sig=self.window_and_pad(w)
# FFT
fft=np.fft.fft(sig)
# Noise suppression
fft = self.subnoise(fft)
# IFFT
res=np.fft.ifft(fft)
# Assume the result is real - ignore the imaginary part
res=np.real(res)
# Remove the padding
res=self.remove_padding(res)
return(res)
def estimate_noise(self,w):
# Compute the padded signal
sig=self.window_and_pad(w)
fft=np.fft.fft(sig)
# Estimate the noise energy
self._noise = np.abs(fft)*np.abs(fft)
# Remove the noise
fft = self.subnoise(fft)
# IFFT and assume the result is real - ignore imaginary part
res=np.fft.ifft(fft)
res=np.real(res)
res=self.remove_padding(res)
return(res)
# Process all the windows using the VAD detection
def remove_noise_from_slices(self):
for (w,v) in zip(self._slices,self._vad):
result=None
if v==1:
# If voice detected, only remove the noise
result=self.remove_noise(w)
else:
# If no voice detected, update the noise estimate
result=self.estimate_noise(w)
self._signal.append(result)
# Overlap and add to rebuild the signal
def overlap_and_add(self):
offsets = range(0, len(self._signal)*winOverlap,winOverlap)
offsets=offsets[0:len(self._signal)]
res=np.zeros(len(data))
i=0
for n in offsets:
res[n:n+winLength]+=self._signal[i]
i=i+1
return(res)
Test this algorithm on the original signal:
n=NoiseSuppressionReference(slices)
n.remove_noise_from_slices()
cleaned=n.overlap_and_add()
plt.plot(cleaned)
plt.show()
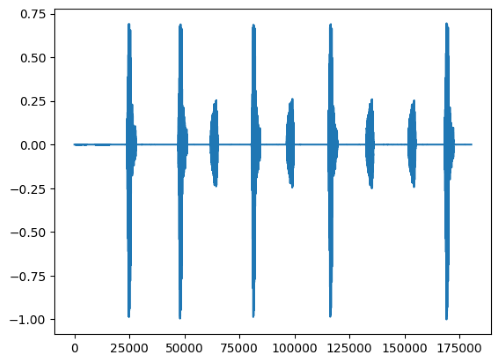Cleaned signal
You can now listen to the result:
audioRef=Audio(data=cleaned,rate=samplerate,autoplay=False)
audioRef
In the next section, you’ll write the optimized version using CMSIS-DSP.