Outer product

Matrix multiplication with the outer product

In this section, you will learn how you can use the outer product with the SME engine to improve matrix multiplication.

In this standard matrix multiplication example, the core of the computation can be represented as:

    

        
        
                acc += matLeft[m * K + k] * matRight[k * N + n];

    

Which translates to 1 multiply-accumulate, which is also known as macc, for two loads (matLeft[m * K + k] and matRight[k *N + n]). It therefore has a 1:2 macc to load ratio.

From a memory system perspective, this is not effective, especially since this computation is done within a triple-nested loop, repeatedly loading data from memory.

To exacerbate matters, large matrices might not fit in cache. In order to improve the matrix multiplication efficiency, the goal is to increase the macc to load ratio, which means to increase the number of multiply-accumulate operations per load.

Figure 3 below shows how the matrix multiplication of matLeft (3 rows, 2 columns) by matRight (2 rows, 3 columns) can be decomposed as the sum of the outer products:

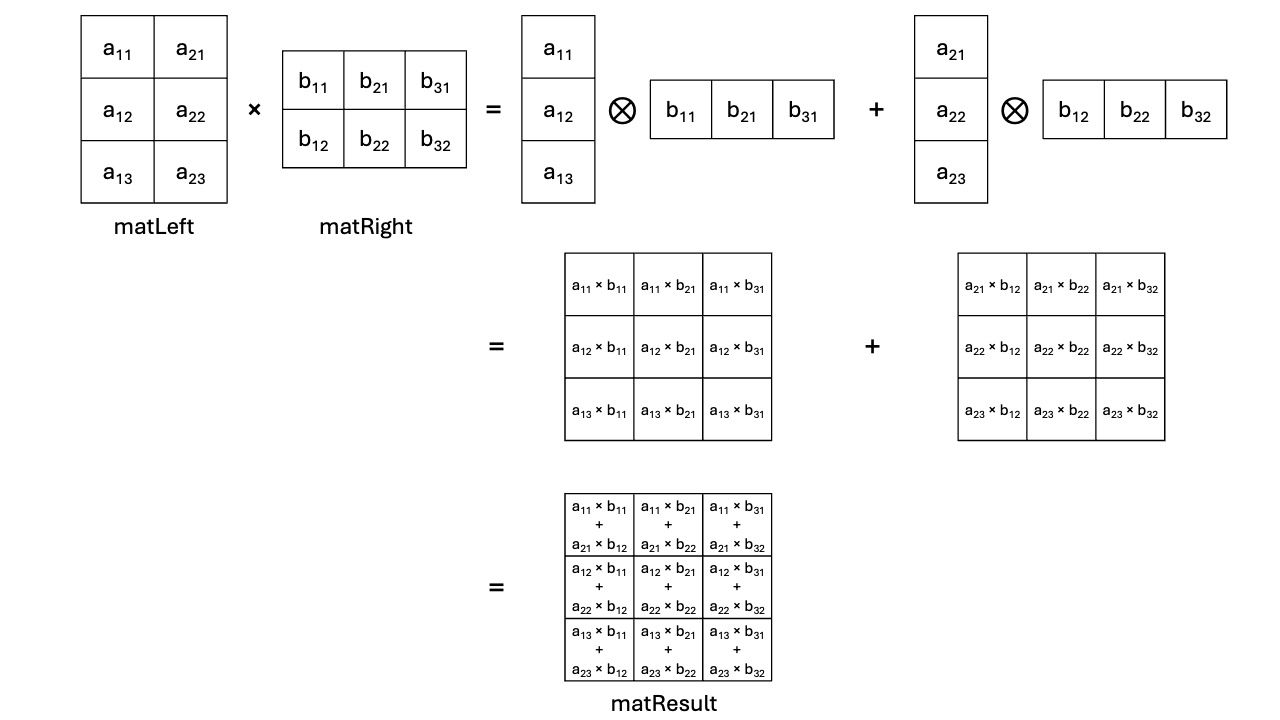Figure 3: Outer Product-based Matrix Multiplication.

The SME engine builds on the Outer Product as matrix multiplication can be expressed as the sum of column-by-row outer products .

About transposition

From the previous page, you will recall that matrices are laid out in row-major order. This means that loading row-data from memory is efficient as the memory system operates efficiently with contiguous data. An example of this is where caches are loaded row by row, and data prefetching is simple - just load the data from current address + sizeof(data). This is not the case for loading column-data from memory though, as it requires more work from the memory system.

In order to further improve the effectiveness of the matrix multiplication, it is therefore desirable to change the layout in memory of the left-hand side matrix, which is called matLeft in the code examples in this Learning Path. The improved layout would ensure that elements from the same column are located next to each other in memory. This is essentially a matrix transposition, which changes matLeft from row-major order to column-major order.

Transposition in the real world

In the same way that trees don’t reach the sky, the SME engine has physical implementation limits. It operates with tiles in the ZA storage. Tiles are 2D portions of the matrices being processed. SME has dedicated instructions to load data to, and store data from tiles efficiently, as well as instructions to operate with and on tiles, for example the fmopa instruction which takes two vectors as inputs and accumulate all the outer products to a 2D tile. The tile in ZA storage is what allows SME to increase the macc to load ratio, as all the tile elements are loaded to the tile, to be used with the SME outer product instructions.

Taking into account that the ZA storage is finite, the desirable transposition of the matLeft matrix that was discussed in the previous section needs to adapted to the tile dimensions, so that a tile is easy to access. The matLeft preprocessing has thus some aspects of transpositions, but takes into account the tiling as well and is referred to in the code as preprocess.

Here is at the algorithmic level what preprocess_l does in practice:

    

        
        
void preprocess_l(uint64_t nbr, uint64_t nbc, uint64_t SVL,
                  const float *restrict a, float *restrict a_mod) {

    // For all tiles of SVL x SVL data
    for (uint64_t By = 0; By < nbr; By += SVL) {
        for (uint64_t Bx = 0; Bx < nbc; Bx += SVL) {
            // For this tile
            const uint64_t dest = By * nbc + Bx * SVL;
            for (uint64_t j = 0; j < SVL; j++) {
                for (uint64_t i = 0; i < SVL && (Bx + i) < nbc; i++) {
                    if (By + j < nbr) {
                        a_mod[dest + i * SVL + j] = a[(By + j) * nbc + Bx + i];
                    } else {
                        // These elements are outside of matrix a, so zero them.
                        a_mod[dest + i * SVL + j] = 0.0;
                    }
                }
            }
        }
    }
}

    

preprocess_l will be used to check the assembly and intrinsic versions of the matrix multiplication perform the preprocessing step correctly. This code is located in file preprocess_vanilla.c.