Vanilla matrix multiplication

Vanilla matrix multiplication

In this section, you will learn about an example of standard matrix multiplication in C.

Algorithm description

The vanilla matrix multiplication operation takes two input matrices, A [Ar rows x Ac columns] and B [Br rows x Bc columns], to produce an output matrix C [Cr rows x Cc columns]. The operation consists of iterating on each row of A and each column of B, multiplying each element of the A row with its corresponding element in the B column then summing all these products, as Figure 2 shows.

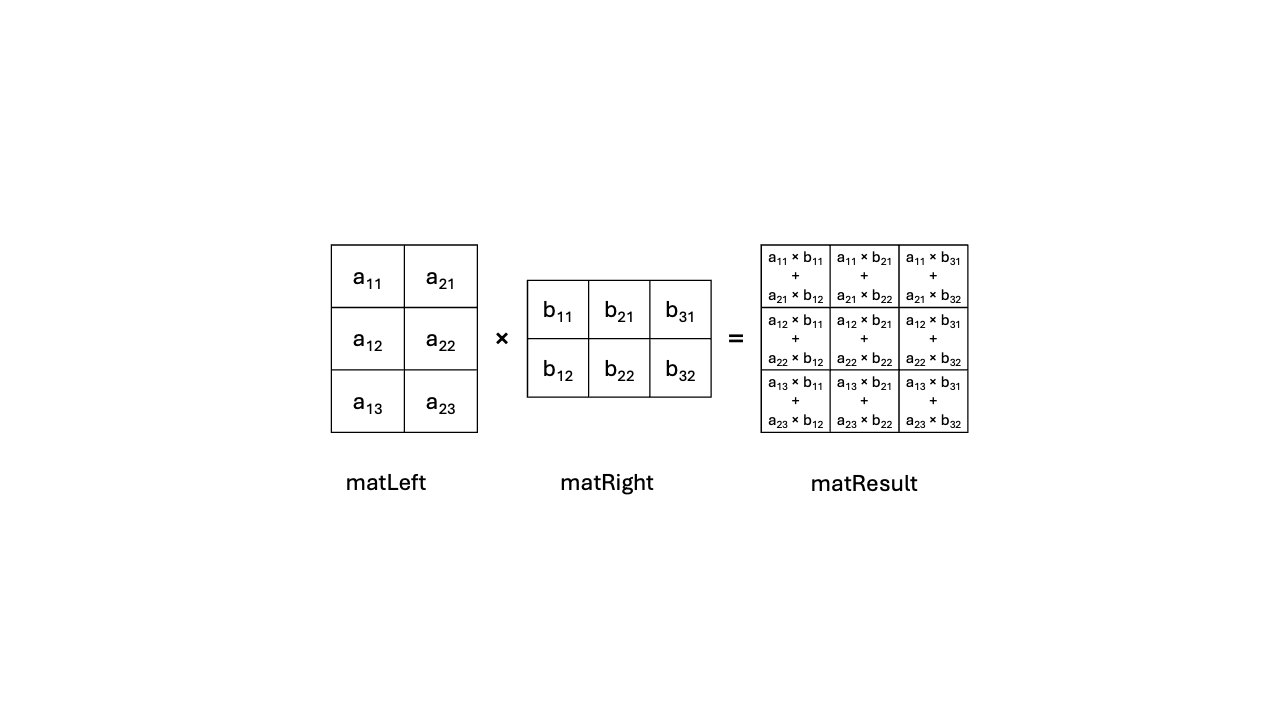Figure 2: Standard Matrix Multiplication.

This implies that the A, B, and C matrices have some constraints on their dimensions:

• A’s number of columns must match B’s number of rows: Ac == Br.
• C has the dimensions Cr == Ar and Cc == Bc.

You can learn more about matrix multiplication, including its history, properties and use, by reading this Wikipedia article on Matrix Multiplication .

In this Learning Path, you will see the following variable names:

• matLeft corresponds to the left-hand side argument of the matrix multiplication.
• matRightcorresponds to the right-hand side of the matrix multiplication.
• M is matLeft number of rows.
• K is matLeft number of columns (and matRight number of rows).
• N is matRight number of columns.
• matResultcorresponds to the result of the matrix multiplication, with M rows and N columns.

C implementation

A literal implementation of the textbook matrix multiplication algorithm, as described above, can be found in file matmul_vanilla.c:

    

        
        
void matmul(uint64_t M, uint64_t K, uint64_t N,
            const float *restrict matLeft, const float *restrict matRight,
            float *restrict matResult) {
    for (uint64_t m = 0; m < M; m++) {
        for (uint64_t n = 0; n < N; n++) {

            float acc = 0.0;

            for (uint64_t k = 0; k < K; k++)
                acc += matLeft[m * K + k] * matRight[k * N + n];

            matResult[m * N + n] = acc;
        }
    }
}

    

In this Learning Path, the matrices are laid out in memory as contiguous sequences of elements, in Row-Major Order . The matmul function performs the algorithm described above.

The pointers to matLeft, matRight and matResult have been annotated as restrict, which informs the compiler that the memory areas designated by those pointers do not alias. This means that they do not overlap in any way, so that the compiler does not need to insert extra instructions to deal with these cases. The pointers to matLeft and matRight are marked as const as neither of these two matrices are modified by matmul.

You now have a reference standard matrix multiplication function. You will use it later on in this Learning Path to ensure that the assembly version and the intrinsics version of the multiplication algorithm do not contain errors.